Quantities in Chemistry: Measurements and Relationships

Dr. Mudassar Altaf, Associate Professor of Chemistry, Department of Higher Education, Government of the Punjab, Pakistan

Contents:

Avogadro number or constant (N_A)
Calculations of particles’ quantity
Molar gas volume (V_m)
Concentrations of solutions
Limiting reactant (reagent)
Yield, percentage yield and types

Avogadro Number or Constant (N_A):

Definition: “The number of particles of a substance present in its one mole equals to 6.022×10²³”, is called Avogadro number or constant.

Particles mean atoms, ions, molecules (covalent compounds) or formula unit (ionic compounds). Imagine what a great number of particles by 1 mole.

1 mole = 6.022 x 10²³
602,200,000,000,000,000,000,000
Six lakh, twenty-two hundred (602200), trillion, trillion.
1 trillion = 10¹². 602,200,000,000=10¹², 000,000,000,000=10¹².
602200 trillion, trillion.
1 lakh crore = 1 trillion; (the count of crore is 1 lakh).
602200 lakh-crore, lakh-crore.
1 trillion = 1000 billion = 1 million-million (the count of million is 1 million). 10 lakh is 1 million; 1 million = 10⁶; 1 billion = 10⁹.

The number of particles in one mole of any substance is the same, but the weight in grams is different, as shown in the following table:

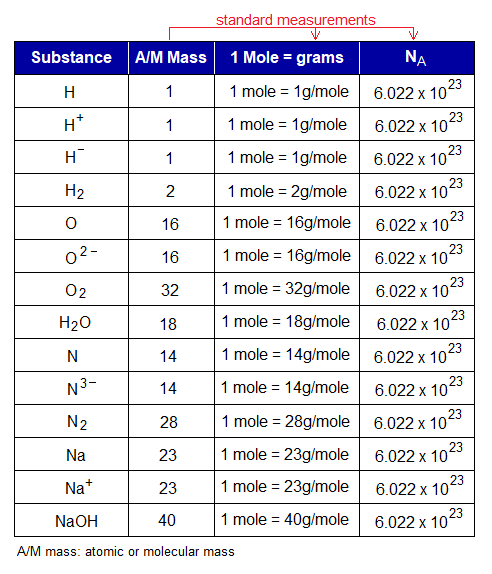
The quantity of the particles is directly related with number of moles. For example, if number of moles are doubled then, the number of particles will also be doubled. For example, one mole of CaCO₃ will contain 6.022×10²³ particles of CaCO₃; however, its 2 moles will contain 2×6.022×10²³= 12.044×10²³ = 1.2044×10²⁴particles. In other words, 100g (1 mole) of CaCO₃ will contain 6.022×10²³ particles; while 200g (2 moles) will contain 1.2044×10²⁴particles. So, number of moles decides the mass in grams as well as quantity of the particles. However, these three are interrelated.

Mole can be abbreviated as M or mol (not to be confused with molecules). Its formula is:

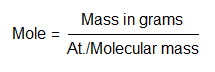
For example, to calculate mass in grams of 1M of NaOH.

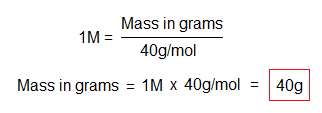
If we take 92g of NaOH, how many moles will it be?

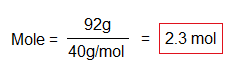
The atomic or molecular mass is a constant value, depending upon the two variables: mole and mass in grams. For example, when 92g of NaOH are divided by 2.3M, then the quotient will be 40g/mol. These two variables are interrelated to keep the third value constant. A comprehensive detail is as under in calculations.

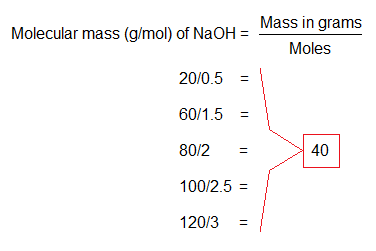
This specific example of NaOH explains that how two variables adjust themselves to keep the molecular mass (40g/mol) a constant number. Likewise, for all other examples the concept is valid.

Exercise 1:

Find out the mass in grams for 1.75M required for H₂SO₃, H₂SO₄, CH₃COOH, H₂S, CO, CO₂, NH₄OH, CaCl₂.
The molecular mass of glucose (C₆H₁₂O₆) is 180g/mol. Find out the weight (mass) in grams required to keep molecular mass 180g/mol as constant with various values of moles. Use 1M, 1.2M, 1.5M, 2M, 10M.

Calculations of Particles’ Quantity:

As mentioned above that 1 mole contains 6.022×10²³particles of any substance either in the form of molecules, formula unit, ions or atoms. The number of particles multiplies by the number of moles. The formula is very simple, just multiply the above one with Avogadro’s number as:

For example, 40g of NaOH will have 1M; because, its molecular mass is 40g/mol; and dividend and divisor are same to yield quotient 1. So, 1 mole of NaOH will calculate number of formula unit (NaOH) 6.022×10²³. As, the number of particles multiplies by the number of moles; so, for any substance, the calculations will be same for atoms, ions, formula unit, or molecules.

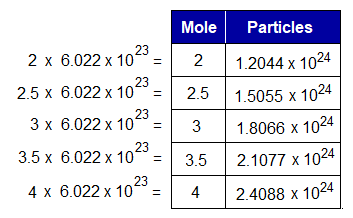
Exercise 2:

Calculate by using formula the number of particles for 10 moles of Na⁺ and Cl^– ions in the solution (the answer is 6.022×10²⁴ for both the ions independently).
Calculate by using formula the number of moles for 1.25×10³⁰ particles of Mg²⁺ ions in the solution (the answer is 2.074×10⁶ moles).

Molar Gas Volume (V_m):

It can be defined as, “the volume occupied by one mole of a gas is 22.414 dm³at room temperature and pressure^”.

The room temperature is 25°Celcius (298 Kelvin); while 1 atmospheric pressure is standard pressure at sea level. The understanding of the volume in cubic shape is as under:

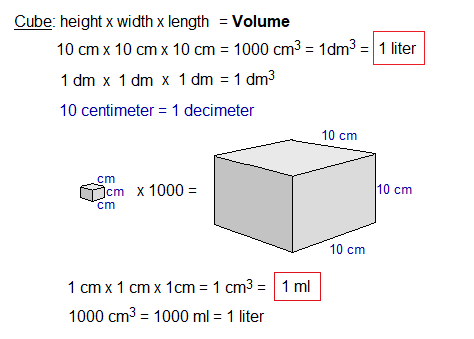
One dm³ is a synonym of one liter (also litre) volume. There are 1000 cm³ in one dm³. So, 22.414 dm³(i.e., 22.414 liters) is equal to 22414 cm³ (i.e., 22414 ml).

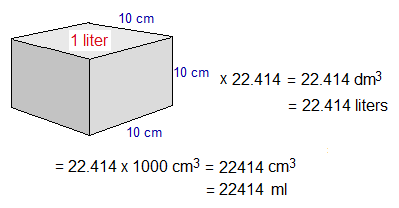
Examples: 1 mole of H₂, CO, CO₂, NH₃, CH₄, C₂H₆, SO₂, O₂, N₂, He, Ne, Ar, Kr, Xe or any other gas occupy 22.414 dm³ (or 22.414 liter; 22414 cm³, 22414 ml) volume at room temperature and pressure (R.T.P.).

A gas enclosed in a cylinder of volume 10 dm³ at R.T.P. Find out its moles.

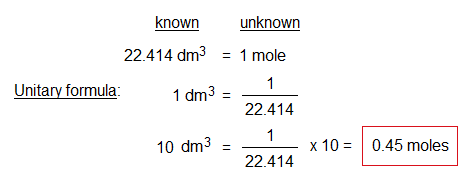
Exercise 3:

Find out the number of moles of gases at 50 dm³ and 75 dm³at R.T.P.
Convert 50 and 75 dm³s in liters, cm³ and ml.
Find out volume in cm³ of a gas at R.T.P. when its 30 moles have been taken in a cylinder.
(a) Find out volume in dm³ of a gas at R.T.P. when its 5 moles have been taken in a cylinder. (b) Also, find out its mass in grams while molecular mass of the gas is 28g/mol. (c) How many molecules will be in there in the cylinder?

Concentrations of Solutions:

The concentration can be defined as, “the amount of a pure substance dissolved in a given volume of the solution”.

In liquids, it can be expressed by g/dm³ or mol/dm³.

Concentration (g/dm³): If the amount of the soluble substance is measured in grams per liter of the solution, then it will be expressed by the unit g/dm³. For example, 7g of table salt (NaCl) dissolved per decimeter cube of the solution. It can be expressed by any unit as following:

7g/dm³ = 7g/liter = 7g/1000 cm³ = 7g/1000 ml

It is not necessary that the volume of solution is always taken as one liter; however, it is a standard. Anyhow, it might be: 5g/500 cm³; 18.4g/200 cm³; or 50g/750 cm³ etc.

Concentration (mol/dm³): If the amount of the soluble substance is measured in moles per liter of the solution, then it will be expressed by the unit mol/dm³. For example, 0.12 moles of NaCl dissolved per dm³ of the solution. Moles=mass in grams/formula mass; 0.12 moles=7g/58.5. So, 7g per liter contains 0.12 moles of NaCl.

0.12 mol/dm³ = 0.12 mol /liter = 0.12 mol /1000 cm³ = 0.12 mol/1000 ml

Exercise 4:

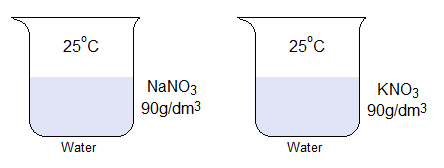
Following the above diagram, find out which solution has higher molar concentration; although, both are equal by g/dm³?
Find out the amount of NaNO₃ required in grams for making its solution 500 cm³with the concentration 90g/dm³.
Find out what amount in grams of KNO₃ required to prepare its 100 ml aqueous solution having the concentration 90g/dm³? Note: It can be solved by using unitary formula.

Example: Prepare an aqueous glucose solution of 500 cm³ with the concentration 1.5 moles per 200 cm³. Note: (1) To measure glucose on the balance, there is a need to convert 1.5 moles into grams. (2) Come to know how much grams are required to adjust concentration 1.5 moles/200 cm³.

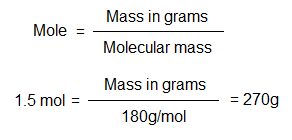
Molecular mass of glucose is 180g/mol. So, its 1 mol will contains 180 grams; and its 1.5 mole will carry 270 grams. In chemistry, the solution calculations are based upon 1000 cm³. Thus, 270g/1000 cm³ the solution will have concentration 1.5 moles. To make a 200 cm³ the solution with this concentration, following calculations will be required.

The amount 54g of glucose dissolved in an aqueous solution of 200 cm³ will have concentration 1.5 moles.

Limiting Reactant (Reagent):

It is defined as:

“The reactant in the chemical reaction that consumes earlier and causes to stop further the reaction; so, a lesser amount of product is formed”.
“The reactant that controls the quantity of the products formed during the chemical reaction”.

There is a standard measurement of reactants for any kind of chemical reaction. How much the amount of the product is required to produce depending upon those standard measurements. If any reactant is added in lesser quantity as per requirement, then that will obviously consume earlier and the second reactant will be left unreacted by its remaining amount. For example, in the chemical reaction between HCl and NaOH, the standard equation will be:

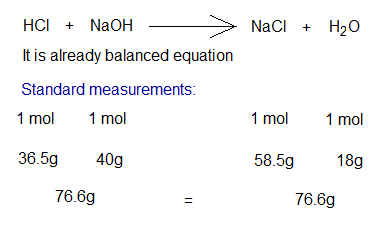
Any further calculation will depend upon above standard values. For, example, if 117g of NaCl is required to prepare, then there will be a need of 73g HCl and 80g of NaOH.

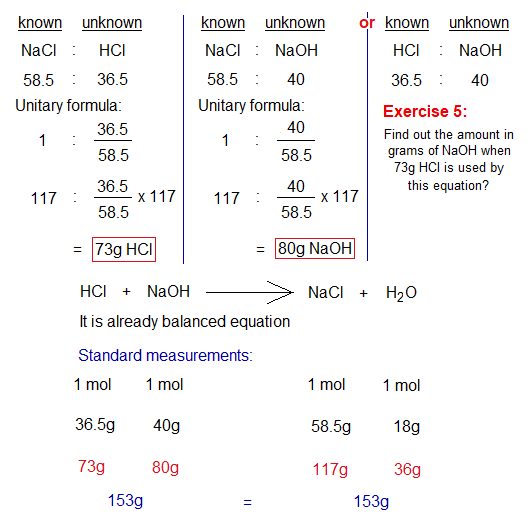
To prepare 117g (2 moles) NaCl, there is a need of 73g (2 moles) HCl with 80g (2 moles) NaOH. However, if 60g (1.65 moles) HCl is taken, then it will be limited reagent according to this calculation. And it will consume first, to produce lesser quantity of the product. So, instead of 117g, only 96.16g (1.65 moles) NaCl will produce by 60g HCl; i.e., 20.84g (0.35 moles) less yield. Similar, is the case with the yield of water.

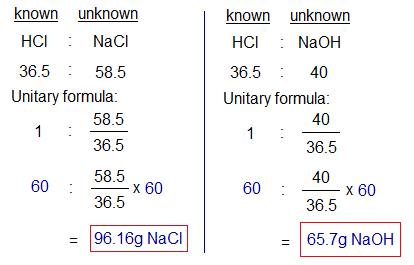
Further, 14.3g (80-65.7) of NaOH will not be used due to non-availability of more HCl. For the same reason, if lesser quantity of NaOH is used than required, it will act as the limiting reactant. In other words, it controls the amount of the product formed.

Exercise 6:

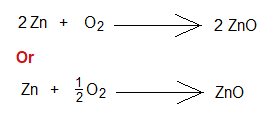
Following is an example of chemical equation. It can be balanced by two ways. Use both equations and write standard measurements in moles and in grams. If Zn is used 0.5 moles; then, explain by calculations in terms of moles and grams that how it will be limiting reactant with standard measurements of O₂. Note: Atomic masses are 65 and 16 g/mol of Zn and O respectively.
Also, calculate how much O₂will remain unreacted.
Also calculate the lesser amount of ZnO produced in terms of moles and grams.

Yield and Percentage Yield:

Chemistry defines yield as, “the quantity of the product obtained as a result of a chemical reaction and is measured in moles or grams”. And the percentage yield is “the quantity of the product obtained as a result of a chemical reaction is measured in percentage”.

Types: It has two types, theoretical and actual yield. These can be defined as:

Theoretical yield: The quantity of the product that is measured from the balanced chemical equation.
Actual yield: The quantity of the product that is measured practically after a chemical reaction. It is also known as experimental yield.

The formula of the yield is as under.

Actual yield is always lesser in amount than theoretical yield due to following reasons. So, the quotient of yield is always less than 1.

Incomplete reactions: Sometimes the reactants don’t react completely, causing a low yield.
Loss during experimental procedure: It is a fact that some loss occurs during transferring the solutions and chemicals from one glassware to another. For example, some drops of the solution remain on the walls of the beaker while transferred into the flask.
Measurement errors: There might be instrumental or human error while measuring the chemicals in measuring cylinder or on balance.
Impurities: Mostly, the chemicals are not 100% pure. So, due to impurities, exact yield is always obtained low but not according to theoretical calculations. There might be a chance of side reactions.

During thermal decomposition of calcium carbonate at 825°C, calcium oxide and carbon dioxide gas are produced. The standard measurements are given below.

Suppose, 100g of CaCO₃is allowed to burn for thermal decomposition. It should produce 56g of CaO as per theoretical calculations. However, the yield is 53g practically. So, let’s find out percentage yield.